5047 - 图论：放东西
小 N 最近在研究 NP 完全问题，小 O 看小 N 研究得热火朝天，便给他出了一道这样的题目：
有 n 个球，用整数 1 到 n 编号。还有 m 个筐子，用整数 1 到 m 编号。每个筐子最多能装 3 个球。
每个球只能放进特定的筐子中。 具体有 e 个条件，第 i 个条件用两个整数 v_i 和 u_i 描述，表示编号为 v_i 的球可以放进编号为 u_i 的筐子中。
每个球都必须放进一个筐子中。如果一个筐子内有不超过 1 个球，那么我们称这样的筐子为半空的。
求半空的筐子最多有多少个，以及在最优方案中， 每个球分别放在哪个筐子中。
小 N 看到题目后瞬间没了思路，站在旁边看热闹的小 I 嘿嘿一笑：“水题！” 然后三言两语道出了一个多项式算法。
小 N 瞬间就惊呆了，三秒钟后他回过神来一拍桌子：“不对！这个问题显然是 NP 完全问题，你算法肯定有错！”
小 I 浅笑：“所以，等我领图灵奖吧！”
小 O 只会出题不会做题，所以找到了你——请你对这个问题进行探究，并写一个程序解决此题。
输入
第一行包含 1 个正整数 T， 表示有 T 组数据。 对于每组数据，第一行包含 3 个正整数 n, m, e， 表示球的个数，筐子的个数和条件的个数。
接下来 e 行，每行包含 2 个整数 v_i, u_i， 表示编号为 v_i 的球可以放进编号为 u_i 的筐子。
输出
对于每组数据，先输出一行，包含一个整数，表示半空的筐子最多有多少个。
然后再输出一行，包含 n 个整数 p_1, p_2, ... , p_n，相邻整数之间用空格隔开，表示一种最优解。其中 p_i 表示编号为 i 的球放进了编号为 p_i 的筐子。 如果有多种最优解，可以输出其中任何一种。
样例
输入
1 4 3 6 1 1 2 1 2 2 3 2 3 3 4 3
输出
2 1 2 3 3
提示
各测试点满足以下约定：
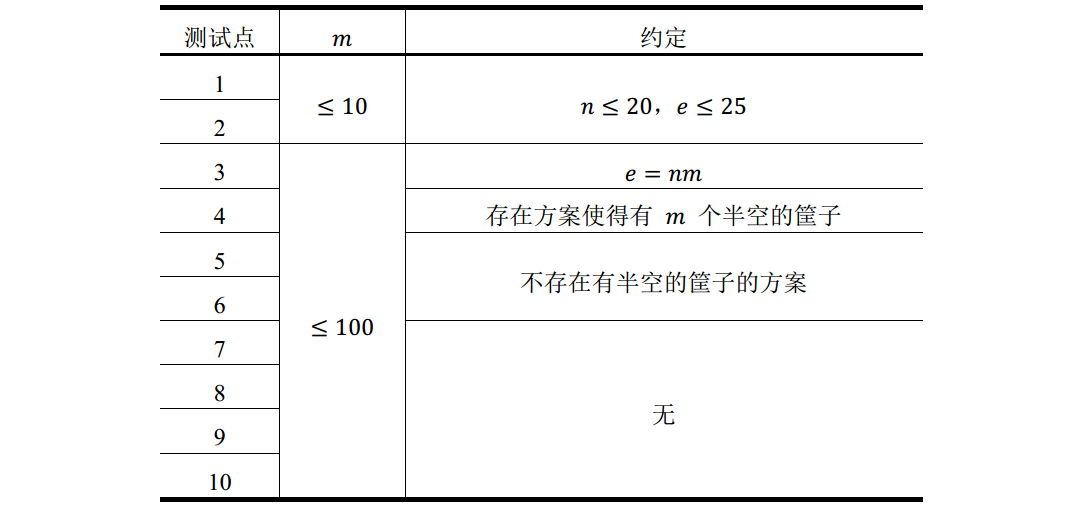
提示
对于所有数据， T \leq 5, 1 \leq n \leq 3m。 保证 1 \leq v_i \leq n, 1 \leq u_i \leq m，且不会出现重复的条件。
保证至少有一种合法方案，使得每个球都放进了筐子，且每个筐子内球的个 数不超过 3。