小杨在探险时发现了一张神奇的矩形地图，地图有 H 行和 W 列。每个格子的坐标是 (r,c)，其中 r 表示行号从 1 到 H，c 表示列号从 1 到 W。 小杨听说地图中隐藏着一些 “黄金格”，这些格子满足一个神秘的数学挑战：当格子坐标 (r,c) 代入特定的不等式关系成立时，该格子就是黄金格。具体来说，黄金格的条件是：

\sqrt{r^2+c^2} \le x + r - c

例如，如果参数 x=5，那么格子 (4,3) 就是黄金格。因为左边坐标平方和的平方根

\sqrt{4^2+3^2}

算出来是 5，而右边 5+4−3 算出来是 6，5 小于等于 6，符合条件。

三行，每行一个正整数，分别表示 h,w,x。含义如题面所示。

一行一个整数，代表黄金格数量。

样例解释 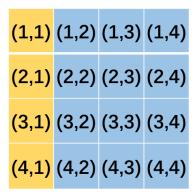图中标注为黄色的四个格子是黄金格，坐标分别为 （1，1），（2，1） ，（3，1） ，（4，1） 。