5973 - NOIP CSP 2025 提高: 第一题 社团招新
小 L 是学校算法协会的成员。在今年的学校社团招新中,小 L 一共招收了 n 个新成员,其中 n 为偶数。现在小 L 希望将他们分到协会不同的部门。
算法协会共设有三个部门,其中第 i (1 \leq i \leq n) 个新成员对第 j (1 \leq j \leq 3) 个部门的满意度为 a_{i,j}。定义一个分配方案的满意度为所有新成员对分配到的部门的满意度之和,也就是说,若将第 i (1 \leq i \leq n) 个新成员分配到了第
d_i \in {1,2,3}
个部门,则该分配方案的满意度为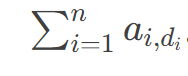 小 L 不希望某一个部门的新成员数量过多。具体地,他要求在分配方案中,不存在一个部门被分配多于
小 L 不希望某一个部门的新成员数量过多。具体地,他要求在分配方案中,不存在一个部门被分配多于
\frac{n}{2}
个新成员。你需要帮助小 L 求出,满足他要求的分配方案的满意度的最大值。
输入
本题包含多组测试数据。
输入的第一行包含一个正整数 t,表示测试数据组数。
接下来依次输入每组测试数据,对于每组测试数据:
- 第一行包含一个正整数 n,表示新成员的数量。
- 第 i+1 (1 \leq i \leq n) 行包含三个非负整数
ai1,ai2,ai3. 分别表示第 i 个新成员对第 1,2,3 个部门的满意度。
输出
对于每组测试数据,输出一行一个非负整数,表示满足小 L 要求的分配方案的满意度的最大值。
样例
输入
3 4 4 2 1 3 2 4 5 3 4 3 5 1 4 0 1 0 0 1 0 0 2 0 0 2 0 2 10 9 8 4 0 0
输出
18 4 13
输入
5 4 9119 2924 6420 9826 12689 7592 7293 16544 12901 11905 18183 18712 4 17699 6268 3841 4695 5271 5018 1276 2321 10572 7708 7645 2620 4 10991 8150 14715 16652 5149 16780 11524 5433 11996 7690 10472 19935 4 8426 4654 16992 16657 13977 18955 10904 9598 9355 873 13468 3146 4 6839 5455 15586 2643 11767 12919 8904 13775 19938 11997 13717 15170
输出
57064 41250 62826 60319 61008
输入
5 10 4839 13582 12308 11875 7476 18522 8568 3134 14491 2198 10410 7327 19052 5127 1171 8008 18004 11221 5628 16009 18854 3941 14230 12173 19429 15426 15290 10974 4717 4732 10 11299 10796 17932 12143 16407 5611 8100 16107 17791 14736 8834 16572 18892 2657 19683 6590 1848 18133 6060 1594 17503 7189 4189 13757 4971 4101 6090 14495 10011 19657 10 15635 12533 16270 11211 2339 16892 6980 3113 19980 13322 9404 16859 8946 1573 16742 1285 5253 2697 16412 5595 18072 15870 17311 7711 11192 4644 19194 6558 1306 10317 10 1561 16149 16433 9399 1760 809 13383 18379 10169 7679 4131 17310 8148 13627 2900 14783 19510 17642 19717 4666 6335 9868 5451 19561 11196 1774 11436 10753 10148 6994 10 1821 19346 18464 7492 8449 19210 5215 9421 17703 7983 8546 11724 12331 13603 13295 13943 19867 9857 18517 15311 10424 1888 2199 17649 10138 14198 15804 2293 13467 18538
输出
157548 158095 151058 156125 170355
提示
说明/提示
【样例 1 解释】
该样例共包含三组测试数据。
对于第一组测试数据,可以将四个新成员分别分配到第 1,3,1,2 个部门,则三个部门的新成员数量分别为 2,1,1,均不超过 \frac{4}{2} = 2,满意度为 4 + 4 + 5 + 5 = 18。
对于第二组测试数据,可以将四个新成员分别分配到第 1,1,2,2 个部门,则三个部门的新成员数量分别为 2,2,0,均不超过 \frac{4}{2} = 2,满意度为 0 + 0 + 2 + 2 = 4。
对于第三组测试数据,可以将两个新成员分别分配到第 2,1 个部门,则三个部门的新成员数量分别为 1,1,0,均不超过 \frac{2}{2} = 1,满意度为 9 + 4 = 13。
【样例 2】
该样例满足测试点 3,4 的约束条件。
【样例 3】
该样例满足测试点 5 \sim 8 的约束条件。
【样例 4】
见选手目录下的 \textbf{\textit{club/club4.in}} 与 \textbf{\textit{club/club4.ans}}。
该样例满足测试点 9 的约束条件。
【样例 5】
见选手目录下的 \textbf{\textit{club/club5.in}} 与 \textbf{\textit{club/club5.ans}}。
该样例满足测试点 15,16 的约束条件。
【数据范围】
对于所有测试数据,保证:
- 1 \leq t \leq 5;
- 2 \leq n \leq 10^5,且 n 为偶数;
- 对于所有 1 \leq i \leq n,1 \leq j \leq 3,均有 0 \leq a_{i,j} \leq 2 \times 10^4。
::cute-table{tuack}
| 测试点编号 | n= | 特殊性质 |
|---|---|---|
| 1 | 2 | 无 |
| 2 | 4 | ^ |
| 3, 4 | 10 | ^ |
| 5 \sim 8 | 30 | ^ |
| 9 | 200 | B |
| 10, 11 | ^ | 无 |
| 12 | 10^5 | A |
| 13, 14 | ^ | B |
| 15, 16 | ^ | C |
| 17 \sim 20 | ^ | 无 |
特殊性质 A:对于所有 1 \leq i \leq n,均有 $a{i,2} = a{i,3} = 0$。
特殊性质 B:对于所有 1 \leq i \leq n,均有 a_{i,3} = 0。
特殊性质 C:对于所有 1 \leq i \leq n,1 \leq j \leq 3,a_{i,j} 均在 [0, 2 \times 10^4] 中独立均匀随机生成。
